
 |
Boost : |
Subject: Re: [boost] different matrix library?
From: Edward Grace (ej.grace_at_[hidden])
Date: 2009-08-15 16:49:07
On 15 Aug 2009, at 18:25, joel wrote:
> Edward Grace wrote:
>> Well, semantics I know but they are all tensors. A
>>
>> scalar -> tensor of order 0,
>> vector -> a tensor of order 1,
>> matrix -> a tensor of order 2. ;-)
> Ok back to this. I had a discussionw ith my co-worker on this
> matter and
> our current code state.
> Well, in fact, in MATLAB, the concept of LinAlg matrix and of
> multi-diemnsional container are merged.
Indeed.
> So now, what about the following class set :
>
> - table : matlab like "matrix" ie container of data that can be
> N-Dimensions. Only suppot elementwise operations.
Ok. Sounds good.
> - vector/covector : reuse table component for memory management + add
> lin. alg. vector semantic. Can be downcasted to table and table
> can be
> explciitly turned into vector/covector baring size macthing.
Yes. By 'table -> vector/covector' do you mean in a similar manner
to 'reshape' in MATLAB? If so good.
> - matrix : ditto 2D lin. alg. object, interact with vector/covector as
> it should. Supprot algebra algorithm. Can have shape etc ...
> - tensor : ditto with tensor.
Yes, I think that makes a lot of sense.
>
> Duck typing + CRTP + lightweight CT inheritance make all these
> interoperable.
Duck typing...... (frantically searches the web)... Hah hah ha!!!
I'd never come across that phrase before, very funny. "Quack Quack"
or should that be "Coin Coin!"?
> Leads to nice stuff like :
>
> vector * vector = outer product
By 'outer product' in the above on the RHS do you mean a matrix or a
specific object of type 'outer product' which is aware of its structure?
As I mentioned before the outer product thus formed will not have N^2
independent components if the two vectors are of length N.
Consequently it could be considered a 'special' type of matrix.
As a concrete example, consider the following, operator (x) is outer
product, . inner (dot) product, I the identity matrix.
this forms a projection operator that, when applied to a vector v
(from the left), will project it on to the orthogonal subspace of k -
(well I think so, I may have made a boo-boo)! As you can see from
the structure of the outer product the number of independent
components in P_k is actually a lot smaller than the total size of
the formed matrix. However, from a typing point of view, what's the
type of Pk - it's clearly not of type 'outer_product'?
So, could we write something like:
P = 2*(identity(4) - outer_product(k,k)/inner_product(k,k));
so that P ends up being aware of its lack of independent components
and acts accordingly?
When dealing with small vector spaces (e.g. R^4) this wouldn't matter
of course - forming a full dense matrix is probably best however if
you are in, say, R^1000 why bother with all the redundant repetition?
[that's a joke b.t.w. 'repetition' is redundant]
> covector * vector = scalar product
Yep.
> vector* covector = matrix
Yep.
> matrix*vector and covector*matrix are properly optimized
> etc...
>
> What do you htink of this then ?
Sounds good to me. When's it finished? ;-)
-ed
------------------------------------------------
"No more boom and bust." -- Dr. J. G. Brown, 1997
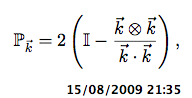
Boost list run by bdawes at acm.org, gregod at cs.rpi.edu, cpdaniel at pacbell.net, john at johnmaddock.co.uk