Geometry Boost List: Re: [geometry] 3D box -> 3D multi_polygon conversion

Subject: Re: [geometry] 3D box -> 3D multi_polygon conversion
From: Barend Gehrels (barend_at_[hidden])
Date: 2013-06-12 06:32:43

Hi,

On 12-6-2013 10:49, Tomislav Maric wrote:
> On 06/12/2013 01:51 AM, Adam Wulkiewicz wrote:
>> Tomislav Maric wrote:
>>> On 06/11/2013 10:12 PM, Adam Wulkiewicz wrote:
>>>> Correct me if I'm wrong but shouldn't ring, polygon, multipolygon,
>>>> etc. be always flat? It may be 3D, may have even some orientation and
>>>> position in 3D space, not only height, but should be flat. This way we
>>>> can perform some 2D operations on it by e.g. first projecting it into
>>>> the 2D plane. E.g. we can calculate convex hull (also flat) or
>>>> triangulate. I'm not so sure if using MultiPolygon concept to describe
>>>> 3D mesh is a good idea. I'd rather provide additional concept.
>>> IMHO this would be quite expensive. Coordinate transform is a Matrix
>>> Vector multiplication, and it costs for nothing, if its only done to
>>> enable 2D calculation on a 3d object. Another point, consider
>>> incremental convex hull in 3D: computing the visible face is not
>>> possible to do this way (mixed product makex only sense for non
>>> co-planar vectors) simply because the hull construction will lie in 3D
>>> and transforming it to 2D projection will not work. I'm sure the
>>> quickhull algorithm is similar.
>>>
>> Sure, this was only an example. My point was that maybe there should
>> be introduced a new, as you've written, MultiPolygon-like concept. And
>> then algorithms should be built for it. Maybe even you'd like to
>> extend MultiPolygon somehow or change it to describe meshes in better
>> way? E.g. should 3D mesh contain faces which are polygons with holes?
>> Or could those containing only triangles be represented in some
>> optimized way?
> Well, I am working on numerical methods for simulating fluid flow, and
> they need flow domain to be decomposed into polyhedra like MultiPolygon,
> so physics prevents the polygons of those polyhedra to have holes...
> What I am aiming at is working on the algorithms in 3D in
> boost.geometry, that I need in order to optimize my geometrical code for
> speed + efficiency, and then extend what I get later for a more general
> purpose.
>
> Triangles: that's a great question actually. Basically, the answer is
> yes and no. Initially the polyhedron is consisted of polygons, but then
> it is decomposed into tetrahedra to compute its volume and do subsequent
> intersections. This is done because some of its polygons will be *non
> planar* (search for voFoam on arXiv.org, page 12 I think).
>
> So, there are three concepts, I believe: polyhedron (multipolygon
> extended), tetrahedron and tetrahedral decomposition of a polyhedron
> (just triangle faces: e.g. optimized normal vector calculation).

The OGC model is our reference model for the concepts point, linestring, 
polygon, multi_point, multi_linestring, multi_polygon. Up to now we have 
followed this model.

See also this webpage, where it can be downloaded:
http://www.opengeospatial.org/standards/sfa

The OGC talks consequently about a "PolyhedralSurface".

I copy a part from the PDF here for convenience:

"
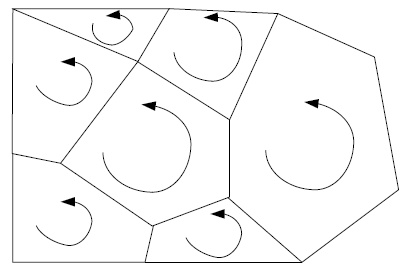
*/6.1.12 PolyhedralSurface/**/
/**/6.1.12.1 Description/**/
/*/A PolyhedralSurface is a contiguous collection of polygons, which 
share common boundary segments. For each//
//pair of polygons that "touch", the common boundary shall be 
expressible as a finite collection of LineStrings. Each//
//such LineString shall be part of the boundary of at most 2 Polygon 
patches. A TIN (triangulated irregular network)//
//is a PolyhedralSurface consisting only of Triangle patches.//
//
For any two polygons that share a common boundary, the "top" of the 
polygon shall be consistent. This means//
//that when two LinearRings from these two Polygons traverse the common 
boundary segment, they do so in//
//opposite directions. Since the Polyhedral surface is contiguous, all 
polygons will be thus consistently oriented.//
//This means that a non-oriented surface (such as Möbius band) shall not 
have single surface representations.//
//They may be represented by a MultiSurface. Figure 14 shows an example 
of such a consistently oriented surface//
//(from the top). The arrows indicate the ordering of the linear rings 
that from the boundary of the polygon in which//
//they are located.//
//
/
/
Figure 14: Polyhedral Surface with consistent orientation//
//
If each such LineString is the boundary of exactly 2 Polygon patches, 
then the PolyhedralSurface is a simple,//
//closed polyhedron and is topologically isomorphic to the surface of a 
sphere. By the Jordan Surface Theorem//
//(Jordan's Theorem for 2-spheres), such polyhedrons enclose a solid 
topologically isomorphic to the interior of a//
//sphere; the ball. In this case, the "top" of the surface will either 
point inward or outward of the enclosed finite solid.//
//If outward, the surface is the exterior boundary of the enclosed 
surface. If inward, the surface is the interior of the//
//infinite complement of the enclosed solid. A Ball with some number of 
voids (holes) inside can thus be presented//
//as one exterior boundary shell, and some number in interior boundary 
shells.//
/"

Regards, Barend