Geometry Boost List: Re: [geometry] distance between geometries

Subject: Re: [geometry] distance between geometries
From: Barend Gehrels (barend_at_[hidden])
Date: 2013-09-01 13:09:06

Hi,

On 1-9-2013 15:36, Adam Wulkiewicz wrote:
> Hi,
>
> I'd like to expose some functionalities that are currently in 
> index::detail to the user, the algorithms calculating:
> - the shortest and longest comparable distance,

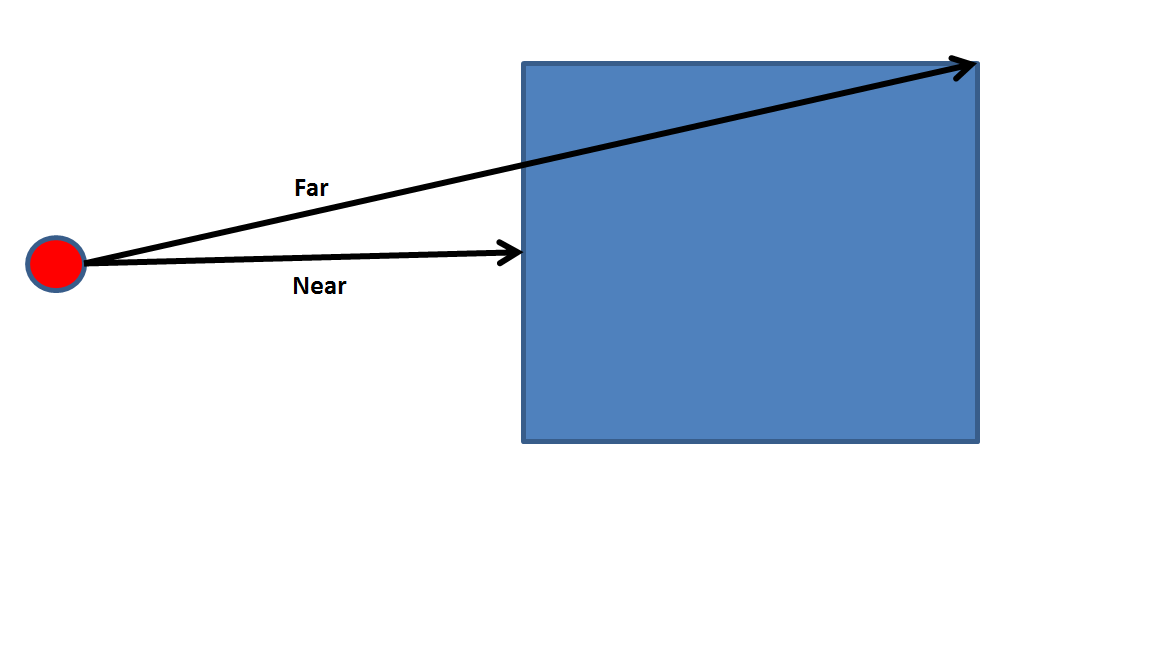
I assume you mean this?

So the shortest is the normal one, what is available as 
boost::geometry::comparable_distance

The longest distance is indeed not yet available as distance or as 
comparable_distance

> - the comparable distance on a path (linestring or segment) to the 
> first intersected geometry from the first path's point or even from 
> some intermediate position on the path.

Do you mean a real intersection, or an object touching or somewhere in 
the neighbourhood?

>
> I'd like to expose them to allow users passing a strategy to nearest() 
> predicate. The user would be able to define how the distance is 
> calculated. The same predicate would work as knn queries (1) or ray 
> queries (2).
>
> The use case would e.g. look like this:
>
> 1. return 5 buildings (Box) nearest to the river (LineString)
>
> tree.query(nearest(river, 5, shortest_distance), out_it);
>
> 2. return 5 bridges (Box) nearest to the begin point(or current 
> location) along the river (LineString) to the north.
>
> tree.query(nearest(river, 5, path_distance), out_it);
> tree.query(nearest(river, 5, path_distance(location)), out_it); // maybe

Where is the North specified? Could you make a small picture such that 
it is crystal clear what is what, and what you exactly mean? Because you 
mention bridges, my question above will probably be answered by a real 
intersection... Do we have already something returning the first houses 
close to the river, following the path?

>
> The user would also be able to use the distance to the Geometry 
> related to the stored bounding box, not only the distance to the 
> bounding box.
That sounds logical to me, this is probably the first thing wanted.
>
> Do you think that they're good candidates not only for the BGI but 
> also for the entire BG? In other words should they be implemented in 
> the boost::geometry or boost::geometry::index namespace? Also do you 
> have an idea for the name? Currently I'm using 
> comparable_distance_near() and comparable_distance_far(). Should they 
> have separate names or e.g. be implemented as bg::comparable_distance 
> with strategy (probably empty)?

The comparable distance is already there. It measures the shortest 
distance. You can specify a strategy there. Comparable distances are 
useful for both cartesian systems (pythagoras) as spherical systems 
(haversine) but not (always) on the Earth, the normal 
distance-calculation is there used as the comparable strategy too.

So the question is: do we want to indicate the point to where we measure 
(shortest, longest) too? For index I think this might be indeed useful 
(you can make queries as "the whole geometry should be located within a 
certain distance"), for the rest I have never had this question.

What has been asked several times is returning not only the distance 
(the shortest distance), but also the point on the polygon where this 
shortest distance is measured. Besides that it is sometimes useful to 
get the distance from a point inside a polygon to the border (which can 
also be expressed using something as distance(point, 
view_as<linestring_tag>(polygon))

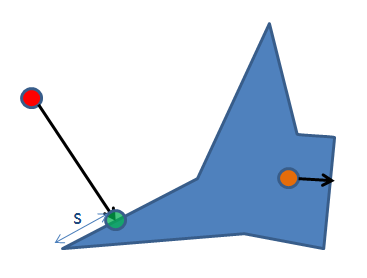
So I started (but it is never submitted to SVN) a "distance_info" 
function, returning 1) the distance from inside (orange point), 2) the 
projected point (green below), 3) the segment on which it occurs, 4) the 
distance on that segment (s below). In case of two linestrings/polygons 
we need to return the 2,3,4 in duplo. In case of multi-polygons we need 
to return to which polygon(s) but that is part of the segment-identifier 
which is already available.

Why I'm saying this now is that we might also add the 
point-to-measure-to (shortest, longest) to this distance_info function 
as an additional parameter. That fits quite well. You would get the 
extra info (2,3,4) to that point then too. These are functionalities 
which are sometimes very useful, but not the first things asked...

There are some additional complexities, because it can well be that a 
point is located on an equal shortest (or longest) distance to two (or 
more) segments of a polygon or linestring, so we might need to return a 
whole collection of projected points...

Regards, Barend