Geometry Boost List: Re: [geometry] distance between geometries

Subject: Re: [geometry] distance between geometries
From: Adam Wulkiewicz (adam.wulkiewicz_at_[hidden])
Date: 2013-09-01 18:04:05

Hi,

Barend Gehrels wrote:
> On 1-9-2013 15:36, Adam Wulkiewicz wrote:
>> I'd like to expose some functionalities that are currently in 
>> index::detail to the user, the algorithms calculating:
>> - the shortest and longest comparable distance,
>
> I assume you mean this?
>
>
>

Yes, also those would be the shortest distances:

> So the shortest is the normal one, what is available as 
> boost::geometry::comparable_distance
>
> The longest distance is indeed not yet available as distance or as 
> comparable_distance
>

I understand that bg::comparable_distance() is intended to work for all 
Geometries and e.g. for cartesian it should return the square of the 
shortest distance between two Geometries. Ok this works for me.

>
>> - the comparable distance on a path (linestring or segment) to the 
>> first intersected geometry from the first path's point or even from 
>> some intermediate position on the path.
>
> Do you mean a real intersection, or an object touching or somewhere in 
> the neighbourhood?

Initially I thought about providing ray queries. Those queries return 
some number of objects hit by a ray.

Because we don't have a Ray concept I decided to use Segment and by 
extension Linestring. I thought about a real intersection because this 
algorithm will probably be the fastest one but more general variations 
could also be useful. I'd like to allow users using any algorithm they 
want in a strategy of the nearest() predicate. More algorithms means 
more possibilities.

Btw, Is this what you've thought?

>
>>
>> I'd like to expose them to allow users passing a strategy to 
>> nearest() predicate. The user would be able to define how the 
>> distance is calculated. The same predicate would work as knn queries 
>> (1) or ray queries (2).
>>
>> The use case would e.g. look like this:
>>
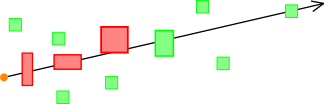
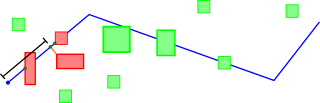
>> 1. return 5 buildings (Box) nearest to the river (LineString)
>>
>> tree.query(nearest(river, 5, shortest_distance), out_it);
>>
>> 2. return 5 bridges (Box) nearest to the begin point(or current 
>> location) along the river (LineString) to the north.
>>
>> tree.query(nearest(river, 5, path_distance), out_it);
>> tree.query(nearest(river, 5, path_distance(location)), out_it); // maybe
>
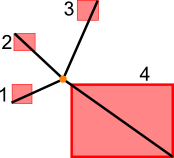
> Where is the North specified? Could you make a small picture such that 
> it is crystal clear what is what, and what you exactly mean? Because 
> you mention bridges, my question above will probably be answered by a 
> real intersection... Do we have already something returning the first 
> houses close to the river, following the path?
>

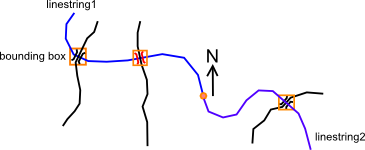
Ah sorry, I was thinking too fast. In this example the river would 
probably have to be divided into two linestrings. First one would go in 
the opposite direction than the second one from some location. The 
second query() call indeed lack the definition of direction.

Well, in the real life the data would probably be stored in some graph 
and knn query won't be needed, nevertheless this is an example of a use 
case.

>>
>> The user would also be able to use the distance to the Geometry 
>> related to the stored bounding box, not only the distance to the 
>> bounding box.
> That sounds logical to me, this is probably the first thing wanted.
>>
>> Do you think that they're good candidates not only for the BGI but 
>> also for the entire BG? In other words should they be implemented in 
>> the boost::geometry or boost::geometry::index namespace? Also do you 
>> have an idea for the name? Currently I'm using 
>> comparable_distance_near() and comparable_distance_far(). Should they 
>> have separate names or e.g. be implemented as bg::comparable_distance 
>> with strategy (probably empty)?
>
>
> The comparable distance is already there. It measures the shortest 
> distance. You can specify a strategy there. Comparable distances are 
> useful for both cartesian systems (pythagoras) as spherical systems 
> (haversine) but not (always) on the Earth, the normal 
> distance-calculation is there used as the comparable strategy too.
>
> So the question is: do we want to indicate the point to where we 
> measure (shortest, longest) too? For index I think this might be 
> indeed useful (you can make queries as "the whole geometry should be 
> located within a certain distance"), for the rest I have never had 
> this question.

The distance in the knn query is used to check which Values are closer 
than the others so in the case of the longest distance it would be used 
to sort nearest geometries by the distance to the furthest point.

I indeed used it to locate Values within some distance and removed this 
possibility because using different predicate - within(circle) is more 
intuitive. Currently I can't find a reasonable use case for it. And to 
be honest this algorithm probably won't be needed, at least by the 
majority of users. Sorry for the confusion.

>
> What has been asked several times is returning not only the distance 
> (the shortest distance), but also the point on the polygon where this 
> shortest distance is measured. Besides that it is sometimes useful to 
> get the distance from a point inside a polygon to the border (which 
> can also be expressed using something as distance(point, 
> view_as<linestring_tag>(polygon))
>
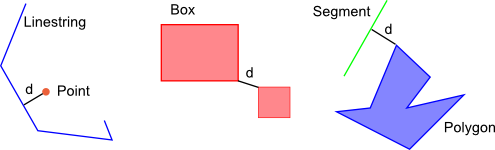
> So I started (but it is never submitted to SVN) a "distance_info" 
> function, returning 1) the distance from inside (orange point), 2) the 
> projected point (green below), 3) the segment on which it occurs, 4) 
> the distance on that segment (s below). In case of two 
> linestrings/polygons we need to return the 2,3,4 in duplo. In case of 
> multi-polygons we need to return to which polygon(s) but that is part 
> of the segment-identifier which is already available.
>
>
>
>
> Why I'm saying this now is that we might also add the 
> point-to-measure-to (shortest, longest) to this distance_info function 
> as an additional parameter. That fits quite well. You would get the 
> extra info (2,3,4) to that point then too. These are functionalities 
> which are sometimes very useful, but not the first things asked...
>
> There are some additional complexities, because it can well be that a 
> point is located on an equal shortest (or longest) distance to two (or 
> more) segments of a polygon or linestring, so we might need to return 
> a whole collection of projected points...

Yes, the knowledge about the position of a measure-point in some cases 
is useful, e.g. in the Linestring example above where the position of a 
closest point must be calculated and then it's distance from the 
beginning of the Linestring.

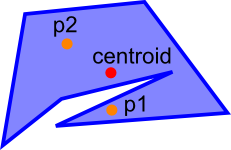
I thought about something related to this and nearest predicate. If we 
have two points inside a Polygon or Two Polygons intersecting one Point, 
which one is the closest?

If I remember correctly, currently I'm using distance = 0 if the Point 
is inside (intersecting) the Box but one could also say that the closest 
one is the one nearest to the centroid or further of the border or even 
something else.

Best regards,
Adam